Classical Planning: #2 TDD a minimum PDDL planner

Implementing a well-performed planning algorithm seems complex, how do we get it start?

Well, PDDL, the Planning Domain Definition Language, describes four things we need to define a search problem:

1. The initial state
2. The actions that are available in a state
3. The result of applying an action
4. The goal state for goal test

So we decompose the problem of implementing planning algorithm into 2 sub-problems:

1. A search algorithm that can find a solution for a given problem, which also defines search problem interface.
2. A PDDL search problem that interprets our PDDL representation.

Then, we choose a relatively simple PDDL problem that fits the following conditions:

1. It has small search space, so that we can start with a simple search algorithm.
2. It is a propositional planning problem, which has no variables defined in the action, so that we can start with a simplified version of PDDL.

Considering all problem examples in the Artificial Intelligence: A Modern Approach (AIMA) book, the Cake problem seems a good fit. Here is the Cake problem described by our PDDL in Ruby (see previous post Classical Planning: #1 PDDL):

{
  init: [[:have, :cake]],
  goal: [[:have, :cake], [:eaten, :cake]],
  solution: [[:eat], [:bake]]
  actions: [
    {
      name: :eat,
      precond: [[:have, :cake]],
      effect: [[:-, :have, :cake], [:eaten, :cake]]
    },
    {
      name: :bake,
      precond: [[:-, :have, :cake]],
      effect: [[:have, :cake]]
    }
  ]
}

(Notice: the Cake problem is from PLANNING GRAPHS section, but we won’t touch planning graph today)

I imbedded solution in above problem description for keeping related information together.

Our first test will look like this:

result = Longjing.plan(cake_problem)
assert !result[:solution].nil?
assert_equal problem[:solution], result[:solution]

Passing this test is today’s goal. We’ll use Child Test strategy described in Test-Driven Development by Example book to reach the goal.

The search algorithm and problem interface

As we discussed above, the first search algorithm we need implement can be simple. So we’ll implement a classical search discussed in chapter 3 “Solving Problems by Searching”of the AIMA book.

Considering graph search is just little bit more complex than tree search, we’ll just go for graph search. For search strategy, we’ll pick breadth-first. Here is new test:

def test_breadth_first_search
  search = Longjing::Search.new(:breadth_first)
  @goal = :g
  ret = search.resolve(self)
  assert_equal [[:move, :a, :d], [:move, :d, :g]], ret[:solution]
  assert_equal [:h], ret[:frontier]
  assert_equal [:a, :b, :c, :d, :e, :f, :g], ret[:explored]
end

In this test, we’re not only caring about the final solution, but also describing the frontier and explored states, so that we know the algorithm used for resolving the problem is the one we expected.

We use TDD strategy Self Shunt to test search algorithm communicates correctly with problem interface. So here is problem interface defined in test:

# problem interface

# ret: state
def initial
  :a
end

# ret: boolean
def goal?(state)
  @goal == state
end

# ret: [action]
def actions(state)
  map = {
    a: [:b, :c, :d],
    b: [:a],
    c: [:e, :f],
    d: [:g],
    e: [:h],
    f: [:h],
    g: [:h],
    h: []
  }
  map[state].map {|to| {name: :move, to: to}}
end

# ret: [action-description]
def describe(action, state)
  [action[:name], state, action[:to]]
end

# ret: state
def result(action, state)
  action[:to]
end

As we expect solution to be a sequence of events [[:move, :a, :d], [:move, :d, :g]] instead of states path, we define an interface method describe(action, state) for converting an exploring event (applying an action to a state) into expected format defined by the problem. (Technically say: we’re hiding data structure of action and state from search algorithm, as problem defines & operates them)

The problem we defined in this test for interacting with search algorithm is a route-finding problem. We define it by symbols along links between them using a Hash in actions(state) method. The following directed-graph describes the map:

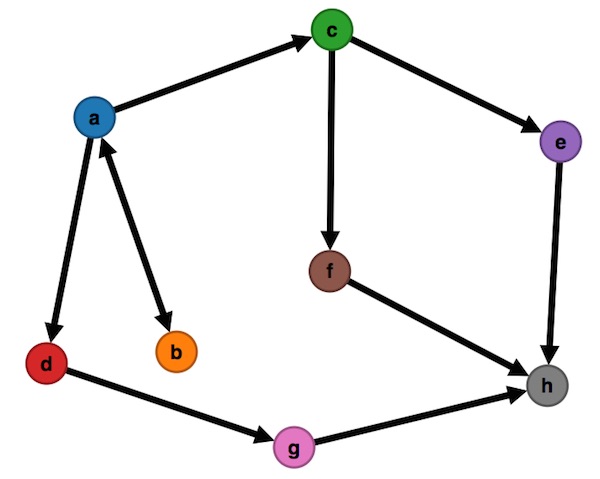
The implementation of search is similar with the graph search described in the chapter 3 “Solving Problems by Searching” of AIMA book, except we construct event sequence as solution. Hence we have a sequences hash to store all sequences of explored and frontier states:

def resolve(problem)
  sequences = {}
  frontier, explored = [problem.initial], Set.new
  solution = nil
  until frontier.empty? do
    state = @strategy[frontier, sequences]
    explored << state

    if problem.goal?(state)
      solution = Array(sequences[state])
      break
    end

    problem.actions(state).each do |action|
      new_state = problem.result(action, state)
      if !explored.include?(new_state) && !frontier.include?(new_state)
        frontier << new_state
        sequence = Array(sequences[state])
        sequences[new_state] = sequence + [problem.describe(action, state)]
      end
    end
  end
  {:frontier => frontier, :explored => explored.to_a, :solution => solution}
end

The breadth-first strategy implementation is also straightforward; as sequences hash has all state sequences, we use it to find out next exploring state having shortest path in frontier:

STRATEGIES = {
  :breadth_first => lambda do |frontier, sequences|
    frontier.sort_by! do |state|
      if seq = sequences[state]
        seq.size
      else
        0
      end
    end.shift
  end
}

Full implementations:

1. search_test.rb
2. search.rb

The PDDL search problem

Now we have clear interface of search problem. PDDL is just another search problem that follows same protocol.

Implementing initial and goal test goal?(state) methods are relatively simple.

Test:

def test_initial
  prob = Longjing.problem(cake_problem)
  assert_equal [[:have, :cake]], prob.initial
end

def test_goal_test
  prob = Longjing.problem(cake_problem)
  assert prob.goal?([[:have, :cake], [:eaten, :cake]])
  assert prob.goal?([[:eaten, :cake], [:have, :cake]])
  assert !prob.goal?([[:eaten, :cake]])
  assert !prob.goal?([[:have, :cake]])
end

(Notice here [:have, :cake] is just one part of whole state. We simply use an Array to represent a state, so a state only contains [:have, :cake] is [[:have, :cake]].)

Implementation:

# longjing.rb
module Longjing
  module_function

  def problem(data)
    Problem.new(data)
  end

# longjing/problem.rb
class Problem
  attr_reader :initial

  def initialize(data)
    @initial = data[:init]
    @goal = data[:goal].sort
    @actions = data[:actions]
  end

  def goal?(state)
    @goal == state.sort
  end

The complexity of PDDL search problem is coming from interpreting action schema in actions(state) and result(action, state) methods. We start with a test like this:

def test_actions
  prob = Longjing.problem(cake_problem)
  actions = prob.actions([[:have, :cake]])
  assert_equal 1, actions.size
  assert_equal :eat, actions[0][:name]
end

Then we’ll look for actions precondition of that matches given state; the only special condition we need handle is negative condition, which starts with :-:

def actions(state)
  @actions.select do |action|
    action[:precond].all? do |cond|
      case cond[0]
      when :-
        !state.include?(cond[1..-1])
      else
        state.include?(cond)
      end
    end
  end
end

(An interesting fact I found in Ruby (2.2): using Array#[1..-1] to get [2, 3] from [1, 2, 3] is faster than using Array#[1] to get [2, 3] from [1, [2, 3]].)

Similarly, here is result(action, state) test to kick off implementing Problem#result:

def test_result
  prob = Longjing.problem(cake_problem)
  state = [[:have, :cake]]
  actions = prob.actions(state)
  ret = prob.result(actions[0], state)
  assert_equal [[:eaten, :cake]], ret
end

The result state should be removing negative literals and adding positive literals in the action’s effects:

def result(action, state)
  action[:effect].inject(state) do |memo, effect|
    case effect[0]
    when :-
      memo - [effect[1..-1]]
    else
      memo.include?(effect) ? memo : memo + [effect]
    end
  end
end

The last method describe(action, state) is also simple, as we don’t have variables defined in action yet.

Test:

def test_describe
  prob = Longjing.problem(cake_problem)
  state = [[:have, :cake]]
  actions = prob.actions(state)
  assert_equal [:eat], prob.describe(actions[0], state)
end

Implementation:

def describe(action, state)
  [action[:name]]
end

Full implementations:

1. problem_test.rb
2. problem.rb

Back to Cake problem

After we sorted out the PDDL search problem, we just need a little more work to hook up everything for solving Cake problem (test passes):

module Longjing
  module_function
  ...
  def plan(problem)
    Search.new(:breadth_first).resolve(self.problem(problem))
  end
end

What’s Next…

Now we have a minimum PDDL planner working, the next step is expending action schema to support variables for describing more complex problems. We’ll aim for solving Blocks World problem in next post and probably start to discovery heuristic function for A* search.